Affichage Public Jeu de l'été 2021 V3.00 ou tout le monde peut poster !!!
Reprise du message précédent
petit lien en passant
https://gamicus.fandom.com/wiki/List_of_Japanese_role-playing_video_games:_1982_to_1987
JIPEMSX :
petit lien en passant
https://gamicus.fandom.com/wiki/List_of_Japanese_role-playing_video_games:_1982_to_1987
https://gamicus.fandom.com/wiki/List_of_Japanese_role-playing_video_games:_1982_to_1987
le jeu s'y trouve
Toute matrice carrée sur un corps K, dont le polynôme caractéristique est scindé, est semblable à une matrice de Jordan. Cette réduction est unique à l'ordre des blocs près. De plus, toute matrice carrée nilpotente sur un corps K est semblable à une matrice de Jordan dont chaque bloc est associé à la valeur 0. Évidement, cette réduction est encore unique à l'ordre des blocs près...
Un jeu publié en 1987
Un bouclier en bois
Un RPG
First-person
DungeonMaster-like
Megarom
Un bouclier en bois
Un RPG
First-person
DungeonMaster-like
Megarom
Toute matrice carrée sur un corps K, dont le polynôme caractéristique est scindé, est semblable à une matrice de Jordan. Cette réduction est unique à l'ordre des blocs près. De plus, toute matrice carrée nilpotente sur un corps K est semblable à une matrice de Jordan dont chaque bloc est associé à la valeur 0. Évidement, cette réduction est encore unique à l'ordre des blocs près...
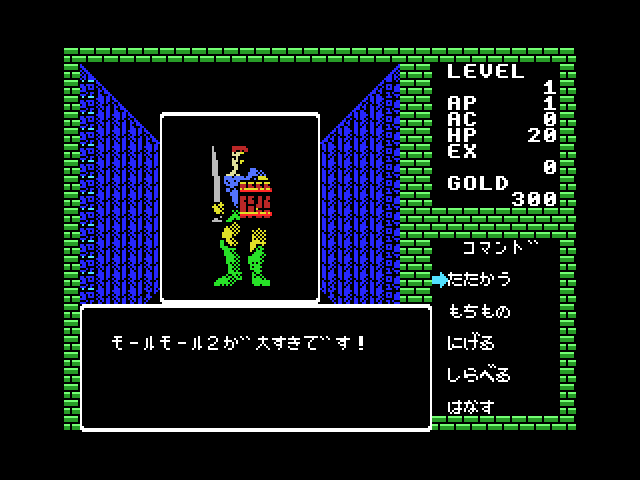
Mole Mole 2 daisuki desu !
Toute matrice carrée sur un corps K, dont le polynôme caractéristique est scindé, est semblable à une matrice de Jordan. Cette réduction est unique à l'ordre des blocs près. De plus, toute matrice carrée nilpotente sur un corps K est semblable à une matrice de Jordan dont chaque bloc est associé à la valeur 0. Évidement, cette réduction est encore unique à l'ordre des blocs près...
Pour celui d'avant, sans conviction : Xanadu, même si il n'y a rien a gagner 
J'ai étudié le cerveau de Sector28
..... Tu verrais le bordel que c'est la dedans 
Mais bon, même si il est bizarre et qu'il aime les pets saveurs poulet, on l'apprécie quand même
Edité par
TurboSEB
Le 13/08/2021 à 20h08
J'ai étudié le cerveau de Sector28
..... Tu verrais le bordel que c'est la dedans Mais bon, même si il est bizarre et qu'il aime les pets saveurs poulet, on l'apprécie quand même
Edité par
TurboSEB
Le 13/08/2021 à 20h08
MSX 1&2 + Moniteurs+divers (environ 0.70Tonnes)
Toute matrice carrée sur un corps K, dont le polynôme caractéristique est scindé, est semblable à une matrice de Jordan. Cette réduction est unique à l'ordre des blocs près. De plus, toute matrice carrée nilpotente sur un corps K est semblable à une matrice de Jordan dont chaque bloc est associé à la valeur 0. Évidement, cette réduction est encore unique à l'ordre des blocs près...
Ghostbusters
Toute matrice carrée sur un corps K, dont le polynôme caractéristique est scindé, est semblable à une matrice de Jordan. Cette réduction est unique à l'ordre des blocs près. De plus, toute matrice carrée nilpotente sur un corps K est semblable à une matrice de Jordan dont chaque bloc est associé à la valeur 0. Évidement, cette réduction est encore unique à l'ordre des blocs près...
Comme tous les autres jeux à license.. c'est une daube !
Toute matrice carrée sur un corps K, dont le polynôme caractéristique est scindé, est semblable à une matrice de Jordan. Cette réduction est unique à l'ordre des blocs près. De plus, toute matrice carrée nilpotente sur un corps K est semblable à une matrice de Jordan dont chaque bloc est associé à la valeur 0. Évidement, cette réduction est encore unique à l'ordre des blocs près...
Toute matrice carrée sur un corps K, dont le polynôme caractéristique est scindé, est semblable à une matrice de Jordan. Cette réduction est unique à l'ordre des blocs près. De plus, toute matrice carrée nilpotente sur un corps K est semblable à une matrice de Jordan dont chaque bloc est associé à la valeur 0. Évidement, cette réduction est encore unique à l'ordre des blocs près...
Répondre
Vous n'êtes pas autorisé à écrire dans cette catégorie